손실 함수까지 공부하고 자러 가야게따 ㅠㅠ 화이팅!
손실 함수를 이해하려면 지도학습의 메카니즘을 알아야 한다고 한다.
지도학습이라고 하는 것은 모델이 학습하는 과정에서 정답을 알려주는 것이다.

- Input 데이터가 들어오면 모델은 데이터를 분석함
- 모델에는 입력층과 은닉층, 출력층, bias로 구성되어 있음
- output은 예측 값임
- 지도학습에서는 실제값과 예측값의 차이를 계산해서 예측을 잘했다 못했다를 판단함
- 예측이 얼마나 정확한지(실제 값과 예측 값이 얼마나 차이 나는지) 나타내는 척도를 손실 함수(Loss Function)라고 함
- 손실 함수가 작아지는 가중치를 찾는 것이 최적화
- 찾은 가중치로 모델을 업데이트함
- 업데이트된 모델에 다시 input을 넣고 output을 내서 예측 값을 확인함
손실 함수의 종류
- 회귀(Regression)
- 우리가 원하는 결괏값이 연속적인 변수인 것을 예측하는 문제
- 집값 예측, 온도 예측
- 단일 숫자, 실수 형태의 값을 얻을 수 있는 문제
- 분류(Classification)
- 우리가 원하는 결괏값이 클래스(class)라고 하는 유한한 모임으로 분류되는 문제
- 질병 예측(양성(1) 또는 음성(0)), 만족도 예측(1, 2, 3점)
- 만족도를 1, 2, 3 이라고 구분 짓는 것을 라벨링(labeling)이라고 함
- 1, 2, 3 숫자들을 라벨(label)이라고 함
- 0과 1로만 구성된 원-핫 벡터(one-hot vector) (1,0,0), (0,1,0), (0,0,1)로 표현하는 방법은 원-핫 인코딩(one-hot encoding)이라고 부름
- 호랑이, 개, 고양이를 0, 1, 2로 나타낼 때 숫자에 대소 관계가 존재하고, 이런 것이 모델에 예상하지 못한 영향을 미칠 수 있기 때문에 0과 1로 만들어진 원-핫 벡터를 사용함
Regression의 대표적인 함수
- 평균 절대 오차(Mean Absolute Error, MAE)
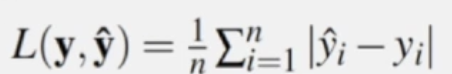
- 예측값과 실제값 차이의 절댓값을 기반으로 한 함수
- 예측값과 실제값의 수직 거리의 평균으로 표현한 함수
- 예측값과 실제값의 거리가 짧으면 손실이 작아짐
- V형 함수라서 미분 불가한 지점이 나옴
- 평균 제곱 오차(Mean Square Error, MSE)

- 예측값과 실제값 차이의 절댓값을 사용하지 않고 두 점의 거리를 이용하여 계산하는 함수
- 예측값과 실제값의 거리가 짧으면 손실이 작아짐
- U형 함수라서 모든 점에서 미분이 가능함
- 제곱식이 들어가기 때문에 절댓값 로스보다는 큰 로스 값이 나올 수 있기 때문에 MAE보다 성능이 좋지 않을 수 있음
- 평균 제곱근 오차(Root Mean Square Error, RMSE)
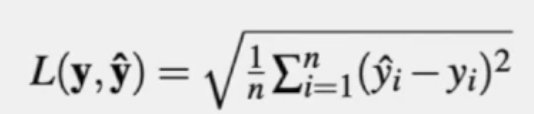
- MSE는 원래 단위를 제곱하여 결과를 내기 때문에, 같은 단위 크기로 만들어 주기 위해 MSE에 제곱근을 씌운 손실 함수
Classification의 대표적인 함수
- 교차 엔트로피 함수(Cross Entropy Function)
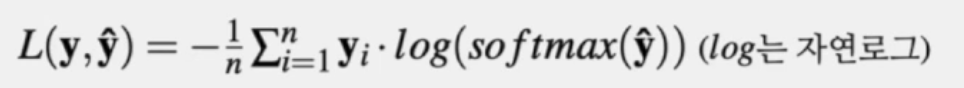
- 분류 문제를 위한 대표적인 손실 함수
- ^y(y_Hat)은 ont-hot vector로 나옴
- 주로 다중 분류에서 사용됨
- 이진 교차 엔트로피 함수(Binary Cross Entropy Function)

- 이진 분류 문제를 위한 교차 엔트로피 함수
- 이진 분류는 두 가지 상황을 분류하는 문제이므로 one-hot vector로 표현하지 않아도 됨
- 그래서 예측하는 단계에서 소프트맥스 함수를 사용하지 않고
- 시그모이드 함수를 사용함
내용에 문제가 있으면 댓글로 알려주세요!
출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)
'딥러닝 공부' 카테고리의 다른 글
| 인공 신경망의 최적화 - 하강법(Descent Method) (0) | 2021.09.23 |
|---|---|
| 인공 신경망의 최적화 - 미분(Differentiation) (0) | 2021.09.23 |
| 인공 신경망 - XOR 문제(XOR Problem) (0) | 2021.09.17 |
| 인공 신경망 - 활성화 함수(Activation Function) (0) | 2021.09.17 |
| 인공 신경망(Artificial Neural Networks) (0) | 2021.09.16 |