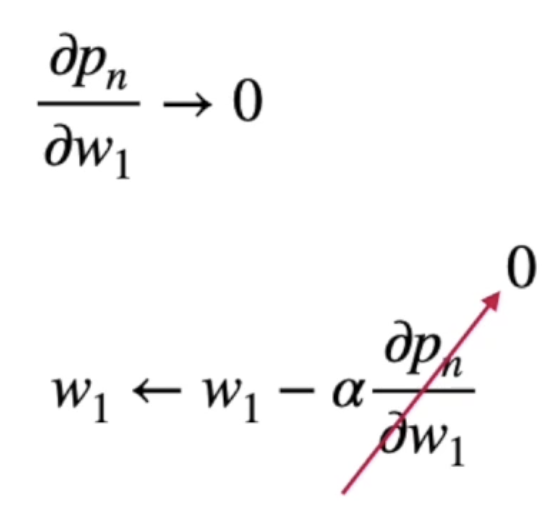MINI

순환 신경망의 다양한 형태들을 알아보쟈

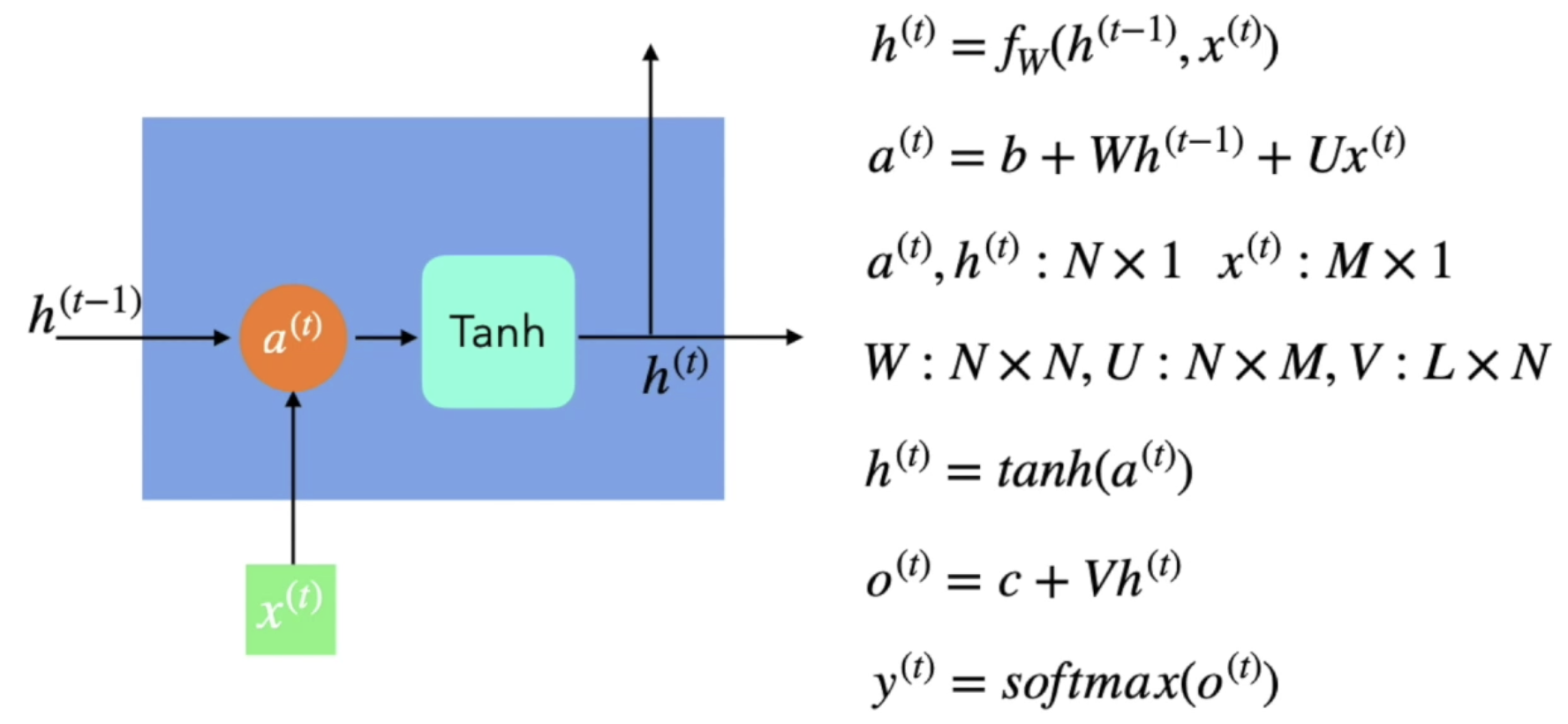
Vanilla RNN

• 이전 hidden state 정보를 받아서 현재 input 값과 계산을 한 뒤에, Tanh라는 activation function을 거쳐서 현재의 hidden statef를 만들어냄
• 이와 같은 방식을 사용하다 보면 '기울기 사라짐' 문제가 발생함

Vanilla RNN의 문제점

• '기울기 사라짐' 문제는 값이 조금만 커지거나 조금만 작아져도 미분 값이 0이 돼버리는 것
• '장기 의존성' 문제는 앞쪽의 hidden state 정보들이 뒷 쪽에 있는 hidden state까지 얼마나 전달이 될까? 라는 의문에서 생겨난 문제

LSTM(Long Short-Term Memory models)

• RNN의 '기울기 사라짐' 문제와 '장기 의존성' 문제를 보완하기 위해 나온 모델
• h값 만 받는 것이 아닌 s라는 gate를 만들어서 문제를 해결함
• 이전 정보를 얼마나 기억할지, 현재 정보를 얼마나 기억할지 구조를 만든 것
• 이전 정보가 덜 중요하다 싶으면 조금만 기억하고, 이전 정보가 중요한 것이면 많이 기억하는 식으로 동작함
• f : forget gate, i : input gate, o : output gate
• sell state, hidden state를 가지고 다음 계산에 반영시킴
• 장점 : 기존 RNN보다 좋은 성능을 가짐
• 단점 : 오래 걸림
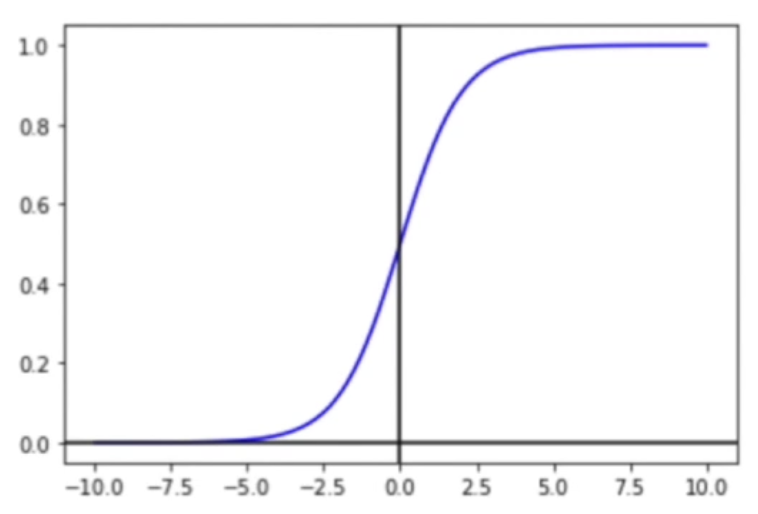
• sigmoid : 항상 0과 1 사이의 값을 가져옴

GRU(Gated Recurrent Unit)

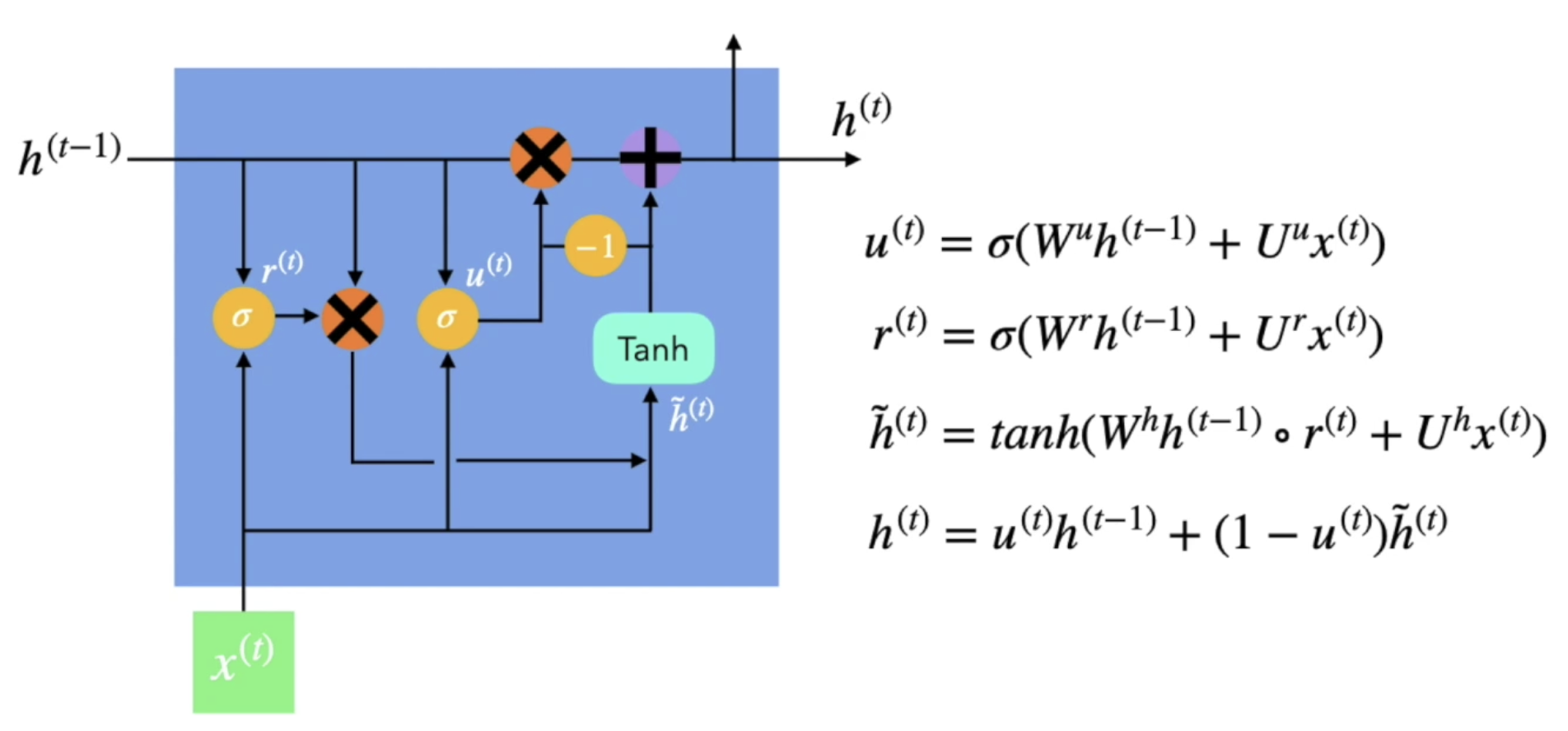
• LSTM 계산이 너무 복잡하니까, 계산을 줄여보자 해서 나온 모델
• r(t)가 0에 가까우면 이전 내용을 거의 반영하지 않겠다는 의미
• r(t)가 1에 가까우면 이전 내용을 많이 반영하겠다는 의미
• 다음으로 넘겨줄 h(t)를 만들 때는, 이전 정보를 살려서 더해주는 형태
• u(t)가 0에 가까우면 이전 정보는 조금, 현재 정보는 많이 반영하겠다는 의미
• u(t)가 1에 가까우면 이전 정보를 많이, 현재 정보를 조금 반영하겠다는 의미

RNN, LSTM, GRU의 근본적인 단점

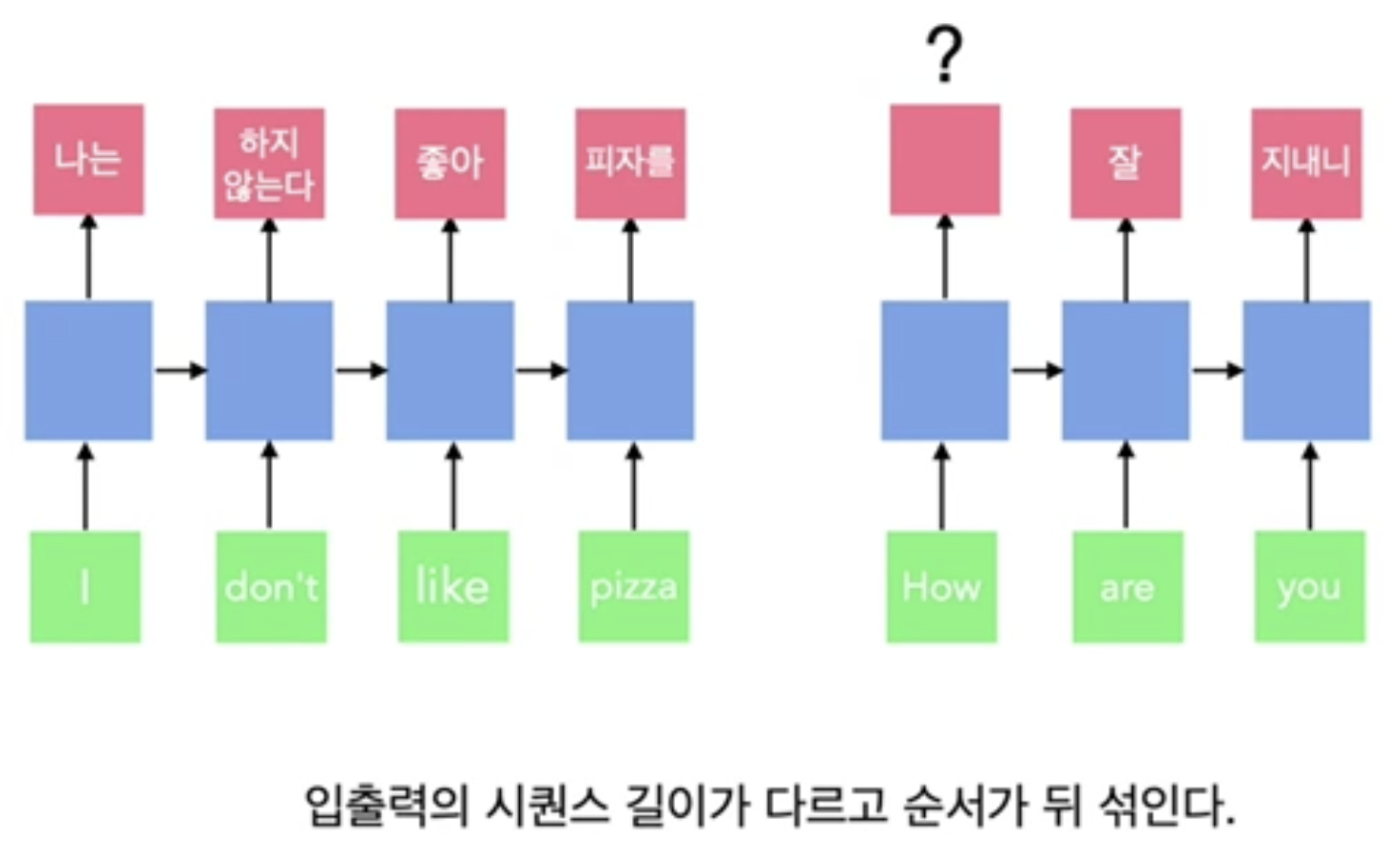
• many to many 번역 문제에서
• 기본적인 RNN 형태에서는 출력 길이를 조절할 수는 있지만 들어오는 문장마다 가변적일 수는 없음
• 순서를 고려하기 쉽지 않음
• 이런 문제를 해결하기 위해 seq2seq(sequence-to-sequence)가 나옴

seq2seq(sequence-to-sequence)

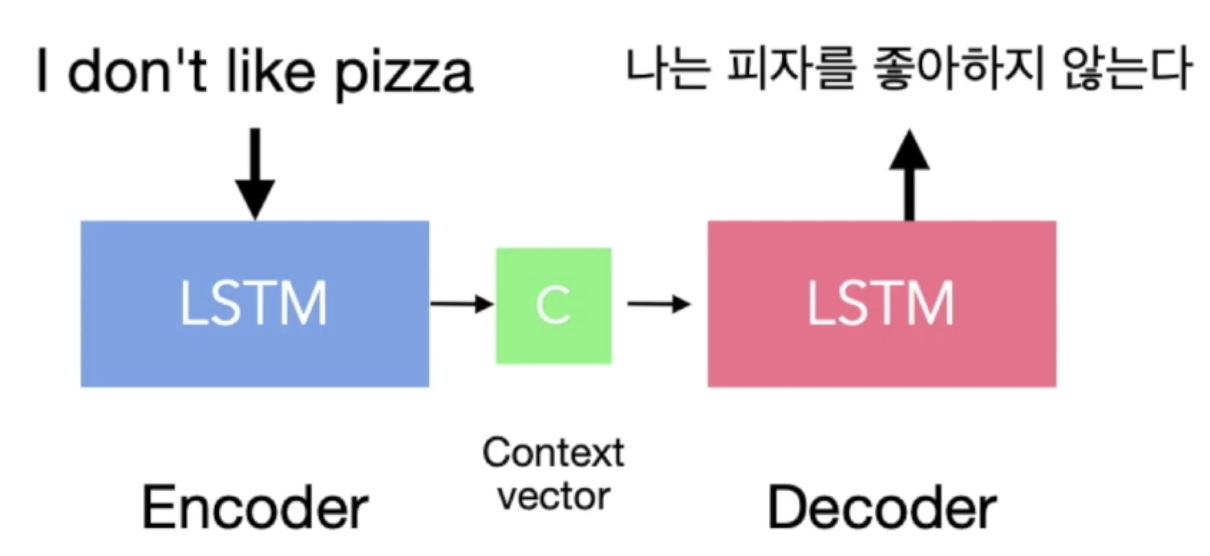
• LSTM 모델 두 개를 붙임
• 앞에 붙은 LSTM 모델을 Encoder라고 하고, 뒤에 붙은 LSTM 모델을 Decoder라고 함
• 입력 값에 대해 LSTM 모델을 통해서 분석을 한 뒤 거기에 대표되는 Context vector를 하나 만듦
• Context vector 정보를 뒤에 붙은 LSTM 모델로 보내서 처리함
• 이렇게 처리하기 때문에 input sequence의 개수와 output sequence의 개수가 달라도 상관없어짐(출력 길이에 구애받지 않음)
• context vector를 받아서 처리하기 때문에 input vector의 순서가 중요하지 않음
• 단점 : 어순을 판단하기 어려움

Attention Mechanism

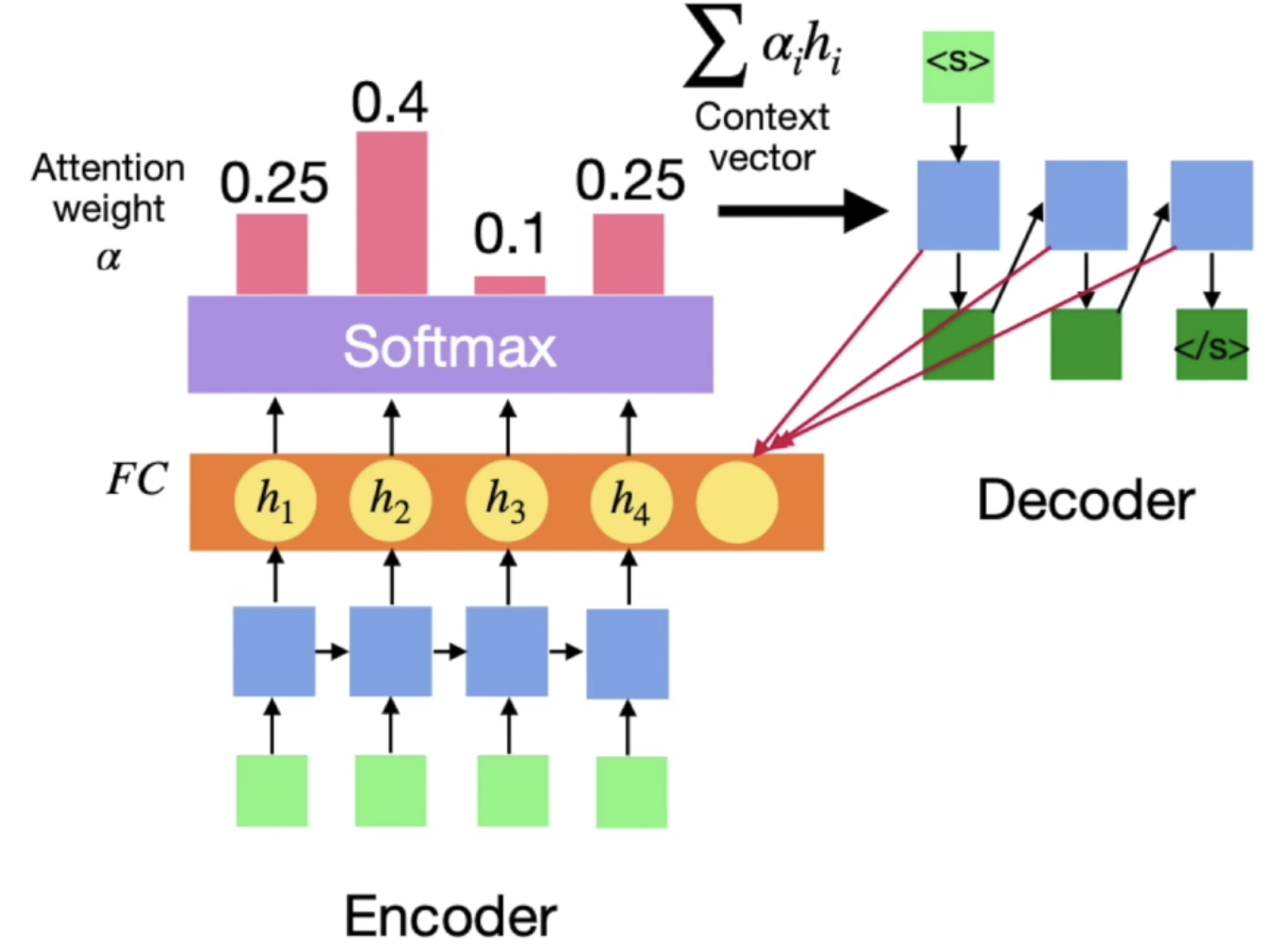
• seq2seq의 어순을 판단하기 어려운 문제점을 해결하기 위해 나옴
• 어순 차이를 극복함
• RNN 연산을 할 때 연산된 각각의 hidden state를 가지고 각각에 가중치를 구해서 hidden state각각에 가중치를 곱해서 더한 값을 context vector로 넘겨줌
• RNN의 고질적인 문제는 현재 정보가 과거의 정보에 영향을 미치지 않는다는 것
• 한 단어 한단어가 번역될 때마다 전체적인 문장에서 가중치를 구함으로서 어순과 상관없이 전체적인 문장을 고려할 수 있음

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)

저녁 운동도 부셨으니, 순환 신경망을 공부해보쟈

순환 신경망의 활용 - 시계열 데이터에 많이 사용됨

1. 언어 번역
2. 신호 처리
3. 주가 예측
4. 음성 인식

일반적인 인공신경망

• input 하나가 모델로 들어오게 되면, 모델이 예측 값을 하나 산출
• 각각의 input 마다 output을 산출

순환 신경망

• input x1이 들어가면 output y1을 산출하는데, 모델에 정보 h1를 저장함
• 두 번째 input  x2가 들어가면 모델에 저장한 정보 h1과 같이 계산을 해서 output y2를 산출함

RNN(Recurrent Neural Network)

1. one to many - x가 들어가서 여러 개의 output을 만드는 것
   • 예를 들어, 작곡 프로그램의 경우 장르가 들어오면 여러 개의 음정을 뽑아냄
2. many to one - 여러개의 데이터를 가지고 하나의 ouput을 산출함
   • 예를 들어, 주가 예측을 하는 경우, 12/1, 12/2, 12/3, 12/4 일의 데이터가 들어갔을 때
   • 12/1의 데이터와 h1(정보)을 이용해서 h2를 만들고
   • 12/2의 데이터와 h2를 이용해서 h3를 만드는 형식으로 감
   • h1, h2, h3, h4와 같은 hidden layer를 sequence라고 부르며, sequence의 길이를 자유롭게 조절할 수 있음
   • 주가 예측할 때, 10일 치를 볼지, 100일 치를 볼지 조절하는 것이 sequence 길이 조정이라고 보면 됨
3. many to mant - 여러 개의 input과 여러 개의 output을 만듦
   • [i][don't][like][pizza] -> one hot encoding으로 변경하여 넣어줌

Vanilla RNN

• 일반적으로 h0 은 영 벡터(0,0,0,...,0,0)로 정의함 
• h => 이전에 있던 hidden state 정보와 현재의 정보를 받아서 현재의 상태를 저장
• o => linear한 인공신경망
• y => 인공신경망에 softmax를 씌워서 output 산출

• h함수는 위 이미지처럼 동작함
• 이전 state인 h(t-1)을 받아서 x(t)와 만나서 연산이 된 것이 a(t)
• a(t)가 activate function인 Tanh를 거쳐서 h(t)를 만듦
• many to many이면 x(t)를 받으면 y^(y_hat)을 만들고
• 그게 아니면 h(t)를 다음으로 넘겨주면 됨

RNN의 손실 함수

• Cross-Entropy : classification 문제에서 많이 사용됨
• MSE : Regression 문제에서 많이 사용됨
• Loss가 가장 작게 나오는 가중치를 구해주면 됨
• 가중치 : W, U, V, c

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)

XOR 문제 다음으로 딥러닝 발전에 암흑기를 가져온 '기울기 사라짐(Vanishing Gradient)'에 대해 공부해본다.

• 인공신경망은 합성함수의 형태로 계산이 되어 결괏값이 나오는 형태이기 때문에, 그 미분은 연쇄 법칙을 통해서 계산이 됨
• 연쇄 법칙은 어떤 미분의 곱들로 계산이 됨
• p1은 활성화 함수 a1에 가중치*x 해준 것
• p1을 w1으로 미분한 값 = a1을 w1으로 미분한 값

• 최종적으로 입력값에 가중치들이 곱해지고 활성화 함수를 미분한 형태들을 볼 수 있음
• 역전파의 형태를 봤더니, 활성화 함수를 미분하는 과정이 들어 있는 것을 알 수 있음

• 빨간색으로 표시된 sigmoid는 스무스한 그래프를 가지고 있음
• sigmoid를 미분하면 파란색 그래프로 표현됨
• sigmoid 미분한 값들을 곱하면 엄청 작은 0에 가까운 수가 됨
• 우리가 구하고자 하는 미분 값이 0에 가까운 수가 될 수 있음

• 우리가 w1에 대해 업데이트하고 싶은데 미분 값이 0으로 가버리게 되면 w1이 되기 때문에
• 다음 가중치가 업데이터 되지 않는 현상이 발생함
• 이 것을 '기울기 사라짐'이라고 함
• 층을 깊게 하면 예측에 좋다고 생각을 했는데, 막상 업데이트를 하려고 하니까 연쇄 법칙이 이뤄지면서 미분 값이 0으로 가버리는 문제가 생김

• ReLU 그래프의 0을 기준으로 왼쪽을 미분하면 0, 오른쪽을 미분하면 1
• 오른쪽 값의 경우 무조건 1이 나오기 때문에 sigmoid 보다는 좋음
• Leaky ReLU 그래프를 사용하여 기울기 사라짐을 더 방지할 수 있음

손실 함수와 최적화에 대해 완벽한 이해가 되지 않더라도, 포인트는 꼭 알고 가자!!

하강법(Descent Method)의 한계

• 손실 함수 설계 시 W형 그래프인 경우 어디가 최솟값인지 알 수 없는 경우가 생기므로 U형 그래프로 설계하는 것이 좋음
• 대표적인 손실 함수(Loss function)의 특징 : MAE, MSE, Cross Entropy 함수는 볼록성(Convexity)을 지님
• Loss Function은 Convex로 설계해주는 것이 가장 좋음

볼록성에 대해서는 아래에서 더 보자!

더보기

볼록성(Convexity)

두 점을 잡아 직선을 그었을 때 원래 있던 함수값보다 위에 있을 경우 Convex라고 이야기함

Loss Function을 Convex 형태로 만들 경우 최솟값을 찾기 쉬우므로 제일 좋음

Non-convex의 경우 시작 위치에 따라 global min으로 갈 수도 있고, local min으로 갈 수도 있기 때문에 최적화하는데 좋지 않음

Loss Function에서 max를 구하는 경우, Concave를 사용하면 좋음(-를 곱하면 min이 되므로 좋음)

 

두 점을 잡아 직선을 그었을 때 원래 있던 함수값보다 위에 있을 경우 Convex라고 이야기함

 

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)

경사 하강법에 대해 알았으니, 확률적 경사 하강법과 최적화 기법에 대해 더 알아보자.

확률적 경사 하강법 : SGD(Stochastic Gradient Descent)

• 이전에 배운 경사 하강법은 Loss가 최소가 되게 하는 w를 찾아서 update 하는 방법이었음
• 경사 하강법의 경우, 데이터가 엄청 클 경우 연산이 엄청 느리고 하드웨어 적으로 메모리가 부족해서 아예 돌아가지 않는 경우가 생기는 문제가 있음
• 이 문제를 해결하기 위해 SGD 방법이 나옴
• 데이터 전체를 넣는 것이 아니고 데이터 전체를 무작위로 섞은 후  mini-batch라는 이름을 가진 것들로 쪼갬
• 그 후 mini-batch를 하나씩 넣어줌
• Loss 값을 구한 후 input이 들어올 때 이전에 들어온 mini-batch의 다음 mini-batch가 들어옴
• 기존 경사 하강법과 확률적 경사 하강법(SGD)의 공식은 똑같음
• SGD의 경우, w를 업데이트 할 때 mini-batch 하나를 가지고 계산한 후 업데이트함

• 경사 하강법과 SGD 공식의 문제점 : 학습률(µ)
• 학습률이 고정된 상수임
• 학습률을 상황에 따라 조절하기 나온 방법이 크게 2가지로 나눠짐
  • 모멘텀 기반 : 공식 뒤에 추가적인 값을 더해주는 것
    1. 보통 감마를 0.9 정도 사용함
    2. 이전 속도를 기억해서 현재에 반영함
  • 가변 학습률 : µ 를 어떤 특정 규칙에 따라 바꿔주는 것
• 모멘텀 기반과 가변학습률을 동시에 적용한 기법 : Adam

Adam(Adaptive Moment Estimation)

• RMSProp와 Momentum 개념을 합친 것
• gradient 자체에 이전 정보를 반영함
• step size 자체에도 이전 정보를 반영함
• 일반적으로 ß1 = 0.9, ß2 = 0.999로 세팅함
• ⍷ 은 10^-8(10의 -8승)으로 세팅함

스케줄링 : µ를 시간에 따라 조절하는 방법

• 스케줄링을 사용할 때 가변 학습률을 사용하지 않고 모멘텀 기법과 함께 사용하거나 일반적인 SGD와 사용함
• StepLR
  • 1-10번째 학습시에는학습 시에는 µ = 10^-3(10의 -3승), 11-20번째 학습 시에는 µ = 10^-4(10의 -4승)을 사용하도록 하는 것
  • 학습 횟수에 따라서 µ를 스케줄링 해놓는 것
  • 계단식으로 줄어드는 것
• ExponentialLR
  • 감마^학습횟수에 µ 를 곱해줌
  • γ^epoch * µ
• Cosine Annealing
  • 일반적으로 스케줄링은 학습을 하면 할수록 작은 학습률을 사용하도록 설계가 되어 있는데
  • 때에 따라서는 큰 값이 필요한 경우도 있기 때문에 Cosine Annealing을 사용함
  • 학습 횟수에 따라서 속도가 줄어들었다가 다시 늘어나고 줄어들었다가 다시 늘어나는 방법

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)

앞에서 하강법에 대해 배웠으니, 경사 하강법에 대해 배워보자.

• 위 이미지를 보면 이전 변수에 새로 계산한 변수로 update 함
• 첫 번째 이미지에서는 µ값을 0.4로 해주었고, 최소 값으로 수렴하는 것을 볼 수 있음
• 두 번째 이미지에서는 µ값을 0.6으로 해주었고, 지그재그로 최솟값을 찾아가는 것을 볼 수 있음
• 세 번째 이미지에서는 µ값을 1.2로 해주었고, 지그재그로 큰 값으로 가는 것을 볼 수 있음
• gradient descent를 사용했음에도 불구하고 최소값을 찾지 못하는 현상이 발생하게 됨
• 따라서, µ 를 적절히  조절을 잘해줘야 함
• µ 이 너무 크면 수렴하지 않을 수 있음
• µ이 너무 작으면 수렴 속도가 너무 오래 걸릴 수 있음

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)

다음은 모델 최적화의 핵심 내용인 경사 하강법을 알기 전에 하강법에 대해 알고 넘어가자.

모델이 어떻게 작동하는지에 대해 알기 위해 메커니즘을 알고 넘어가야 한다.

• 먼저 모델의 input이 주어지면 인풋값을 바탕으로 아웃풋을 산출함
• input 값을 받아서 output 값을 추출하는 것을 '예측'이라고 함
• 예측 값이 실제 값과 얼마나 차이가 나는지 아는 것이 중요
• 실제 값과 예측 값의 차이를 나타내는 척도가 Loss Function
• 실제 값과 예측 값의 차이가 작으면 작을 수록 학습이 잘 되고 있다는 것
• w라는 변수를 가지고 있는 모델을 거쳐서 나온 예측 값을 Loss Function에 넣었을 때 값이 작게 나오면 학습이 잘 되고 있는 것
• 그렇기 때문에, Loss Function의 값이 작게 나오게 하기 위한 w를 구해서 모델에서 사용하는 w값을 update 함
• 위 이미지의 과정(점점 좋은 w값을 찾는 것)을 반복하는 것을 '최적화'라고 함
• 모델의 파라미터를 최적화하는 것을 최적화라고 하는데, Loss Function의 값을 작게 만들어주는 w를 찾는 과정이라고 볼 수 있음
• 일반적으로 초기의 값은 임의로 주어짐
• 가끔 Loss Function에서 min이 아닌 max를 구하는 로직이 있는데, 이럴 때 당황하지 말고 -max(loss)를 취해주자
• max(loss) = -min(loss)

목적 함수(Objective Function)

• Loss Function을 작게 하는 모델의 변수를 구하는 것이 목적
• 그래서 위 함수를 목적 함수라고 부름
• 목적함수를 기준으로 해서 w값을 계속 갱신함

하강법(Descent Method)

• 주어진 지점으로부터 더 작은 곳으로 이동하려는 방법을 하강법이라고 함
• 그림의 오른쪽 지점에서 미분을 하면 양수의 기울기가 나오고, 왼쪽 지점에서 미분을 하면 음수의 기울기가 나옴
• w 지점이 내려가는 방향의 부호와 접선의 기울기가 항상 다름

• 

  이 부등호를 만족하는 방향으로 간다면, 항상 아래쪽으로 향할 수 있음

• 하강법의 단점 - 초기 위치에 따라서 도착 지점이 달라질 수 있음(local min에 도착할 수 있음)
• 우리의 목표는 global min으로 가는 것임
• 딥러닝에서 global min으로 가도록 하는 것은 매우 힘든 일

• 보통 경사 하강법을 주로 사용함
• 속도는 느리지만 좀 더 정확한 계산을 원한다면 뉴턴 방법을 사용함

경사 하강법(Gradient Descent)를 살짝 맛보고 넘어가 보자.

• 앞의 내용들을 통해서 경사 하강법이 나옴
• 경사 하강법을 사용할 때는 이전 변수(w)에서 step size(µ)에 이전 변수의 gradient 값(▽f(w))을 빼서 다음 step으로 가게 함

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)

추석 연휴가 다 지나갔으니 다시 겅부를 시작해보쟈ㅠ

오늘은 미분에 대해 공부해볼 예정이다.

미분은 인공신경망을 최적화하는데 가장 핵심 요소이기 때문에 반드시 알아야 한다고 한다.

기울기의 정의?

• 직선의 가파른 정도 (두 점을 알고 있어야 기울기를 구할 수 있음)
• y = ax + b => a : 기울기
• 접선의 기울기를 알기 위해서 하나의 점에서 가까운 점들을 하나씩 넣어서 기울기를 구해서 극한으로 보냄
• 왼쪽 그림에서 초록색으로 나타낸 부분은 '평균 기울기'라고 부르며,
• 오른쪽 그림에서 표시된 접선의 기울기는 '순간 기울기'라고 부름

도함수와 미분 계수

• x와 y에 대한 도함수
• 도함수는 순간 기울기를 의미함

미분법 종류

• 곱의 미분법

• 합성 함수의 미분법

연쇄 법칙(Chain Rule)

• 인공 신경망은 기본적으로 합성함수의 연산임
• 미분 가능한 함수들의 합성함수를 미분하는 법칙

그레디언트(Gradient)

• 함수 f를 변수 별로 한 번 미분한 것들을 모은 벡터

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)

손실 함수까지 공부하고 자러 가야게따 ㅠㅠ 화이팅!

손실 함수를 이해하려면 지도학습의 메카니즘을 알아야 한다고 한다.

지도학습이라고 하는 것은 모델이 학습하는 과정에서 정답을 알려주는 것이다.

• Input 데이터가 들어오면 모델은 데이터를 분석함
• 모델에는 입력층과 은닉층, 출력층, bias로 구성되어 있음
• output은 예측 값임
• 지도학습에서는 실제값과 예측값의 차이를 계산해서 예측을 잘했다 못했다를 판단함
• 예측이 얼마나 정확한지(실제 값과 예측 값이 얼마나 차이 나는지) 나타내는 척도를 손실 함수(Loss Function)라고 함
• 손실 함수가 작아지는 가중치를 찾는 것이 최적화
• 찾은 가중치로 모델을 업데이트함
• 업데이트된 모델에 다시 input을 넣고 output을 내서 예측 값을 확인함

손실 함수의 종류

1. 회귀(Regression)
   • 우리가 원하는 결괏값이 연속적인 변수인 것을 예측하는 문제
   • 집값 예측, 온도 예측
   • 단일 숫자, 실수 형태의 값을 얻을 수 있는 문제
2. 분류(Classification)
   • 우리가 원하는 결괏값이 클래스(class)라고 하는 유한한 모임으로 분류되는 문제
   • 질병 예측(양성(1) 또는 음성(0)), 만족도 예측(1, 2, 3점)
     • 만족도를 1, 2, 3 이라고 구분 짓는 것을 라벨링(labeling)이라고 함
     • 1, 2, 3 숫자들을 라벨(label)이라고 함
     • 0과 1로만 구성된 원-핫 벡터(one-hot vector) (1,0,0), (0,1,0), (0,0,1)로 표현하는 방법은 원-핫 인코딩(one-hot encoding)이라고 부름
     • 호랑이, 개, 고양이를 0, 1, 2로 나타낼 때 숫자에 대소 관계가 존재하고, 이런 것이 모델에 예상하지 못한 영향을 미칠 수 있기 때문에 0과 1로 만들어진 원-핫 벡터를 사용함 

Regression의 대표적인 함수

1. 평균 절대 오차(Mean Absolute Error, MAE) 

   

   • 예측값과 실제값 차이의 절댓값을 기반으로 한 함수
   • 예측값과 실제값의 수직 거리의 평균으로 표현한 함수
   • 예측값과 실제값의 거리가 짧으면 손실이 작아짐
   • V형 함수라서 미분 불가한 지점이 나옴
2. 평균 제곱 오차(Mean Square Error, MSE)

   

   • 예측값과 실제값 차이의 절댓값을 사용하지 않고 두 점의 거리를 이용하여 계산하는 함수
   • 예측값과 실제값의 거리가 짧으면 손실이 작아짐
   • U형 함수라서 모든 점에서 미분이 가능함
   • 제곱식이 들어가기 때문에 절댓값 로스보다는 큰 로스 값이 나올 수 있기 때문에 MAE보다 성능이 좋지 않을 수 있음
3. 평균 제곱근 오차(Root Mean Square Error, RMSE)

   

   • MSE는 원래 단위를 제곱하여 결과를 내기 때문에, 같은 단위 크기로 만들어 주기 위해 MSE에 제곱근을 씌운 손실 함수

Classification의 대표적인 함수

1. 교차 엔트로피 함수(Cross Entropy Function)

   

   • 분류 문제를 위한 대표적인 손실 함수
   • ^y(y_Hat)은 ont-hot vector로 나옴
   • 주로 다중 분류에서 사용됨
2. 이진 교차 엔트로피 함수(Binary Cross Entropy Function)

   

   • 이진 분류 문제를 위한 교차 엔트로피 함수
   • 이진 분류는 두 가지 상황을 분류하는 문제이므로 one-hot vector로 표현하지 않아도 됨
   • 그래서 예측하는 단계에서 소프트맥스 함수를 사용하지 않고
   • 시그모이드 함수를 사용함

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)

XOR 문제는 무엇인가..? XOR 문제에 대해 알아보쟈ㅑㅑㅑㅑ

XOR 문제란?

• XOR 연산을 기존에 있던 퍼셉트론 알고리즘을 가지고 풀 수 있느냐 없느냐에 대한 문제
• 퍼셉트론 형태는 선형식 형태임
• 어떤 직선을 그려도 빨간색은 빨간색끼리, 파란색은 파란색끼리 나눌 수 없음
• MLP로 해결함
• 은닉층을 사용해서 해결함

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)

달린다, 공부, 배운다, 활성화 함수

모델의 정확도를 높여주는 활성화 함수에 대해 알아보자.

• ^y(y_Hat)는 x에 대해서 표현이 가능함
• ^y(y_Hat)는 x에 대한 1차식으로 표현됨
• 수학적으로 생각해보면 인공신경망은 기본적으로 1차 결합 형태의 함수가 합성된 합성 함수의 연산이라고 볼 수 있음
• 1차식은 미분이 매우 쉽다는 장점이 있음
• 비선형적인 관계가 많기 때문에, 비선형적인 관계를 표현할 수 있도록 만든 장치가 활성화 함수임

• 은닉층(h1)에 값을 넣기 전에 활성화 함수를 한번 태운 후 넣어줌
• 각 층마다 활성화함수의 종류가 다를 수도 있음

활성화 함수란?

• 활성화 함수는 각 층의 관계를 비선형 관계로 만들어주기 때문에 기본적으로 비선형 함수임
  1. 선형(linear) 함수 

     

     • 직선을 의미함
     • a(x) = ax + b 형태로 나타낼 수 있음
  2. 시그모이드(sigmoid) 함수

     

     • 각 층의 관계를 비선형적으로 만들어줌
     • 미분 가능함 
     • 0과 1사이의 값을 취함
     • 0과 1사이의 값들로 이루어져 있기 때문에 0.5 초과면 1로 표현하고, 0.5 이하면 0으로 표현함
     • 이진 분류(binary classification) 문제에 활용이 가능함
     • 다중 분류 문제에서도 활용이 가능함
  3. 하이퍼블릭 탄젠트(tanh) 함수

     

     • 시그모이드(sigmoid) 함수와 비슷함
     • 미분 가능함
     • -1 과 1 사이의 값을 취함
     • 0 주변에 경사가 가파르기 때문에 미분 시 시그모이드(sigmoid) 함수보다 높은 값이 나올 수 있음
  4. ReLU(Rectified Linear Unit) 함수

     

     • 가장 많이 쓰이는 활성화 함수
     • 음수 값이 들어오면 0이 되고, 양수 값이 들어오면 그 값을 그대로 보냄
     • 예를 들어, -2 가 들어오면 ReLU 함수를 거쳐서 0으로 내보내지고, 5가 들어오면 ReLU 함수를 거쳐서 5로 내보내 짐
     • 두 개의 직선을 이어 만든 것으로 비선형 함수지만 선형과 매우 유사한 성질을 가지고 있음
     • 계산이 쉽고 미분도 쉬움
     • 0 지점은 미분이 불가능하기 때문에 0일 경우 어떻게 처리할지 정해줘야 함
  5. Leaky ReLU 함수

     

     • 마이너스 값도 취할 수 있는 ReLU 함수
  6. ELU(Exponential Linear Unit) 함수

     

     • Leaky ReLU 함수의 직선 부분을 곡선으로 변경한 함수
     • 음수의 미분 값이 각 지점마다 차이가 있음 
  7. 소프트맥스(Softmax) 함수
     • 분류 문제에 최적화된 함수
     • 모든 input 값들에 대해서 0과 1 사이의 값이 나옴
     • 모든 성분의 합이 항상 1이 나옴 = 확률처럼 사용 가능
     • 이전 노드의 값이 음수가 나오지 않게 하기 위해 항상 0과 1 사이의 값이 나오도록 함

내용에 문제가 있으면 댓글로 알려주세요!

출처 : 인프런 - 실전 인공지능으로 이어지는 딥러닝 개념 잡기(딥러닝 호형)